23、二叉树基础(上)
思考:二叉树有哪几种存储方式?什么样的二叉树适合用数组来存储?
主要内容
树:一种非线性表结构
树定义
以图说树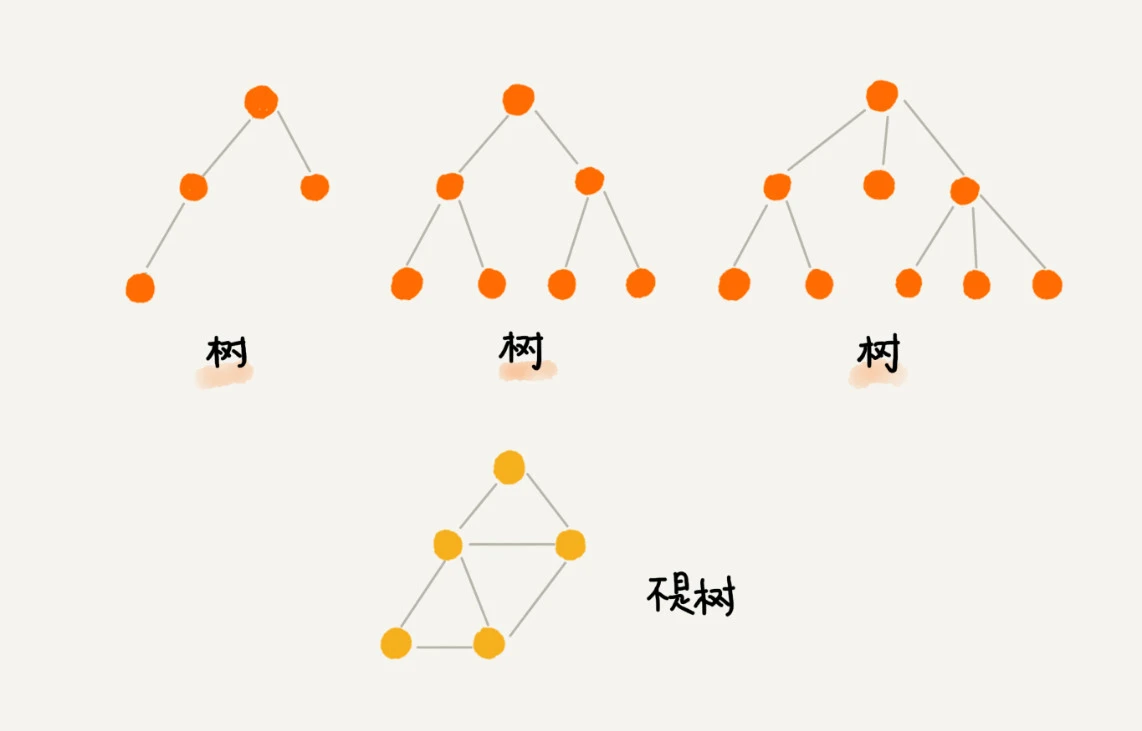
树中的每个元素称为节点,通过父级节点来连接相邻节点。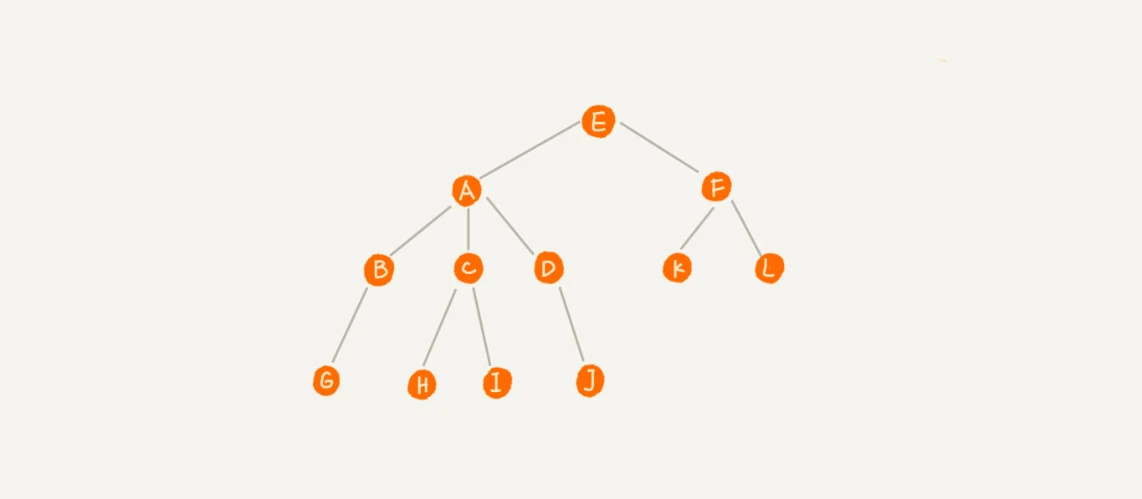
没有父节点的 E 称为根节点
A 是 E 的子节点,E 是 A、F 的父节点
A、F 有相同父节点的称为兄弟节点
没有子节点的 K、L、 G、H、I、 J 都称为叶子节点/叶节点
节点的高度 = 这个节点到叶子节点的最长路径(边数)
节点的深度 = 根节点到这个节点所经历的边的个数
节点的层数 = 节点的深度 + 1
树的高度 = 根节点的高度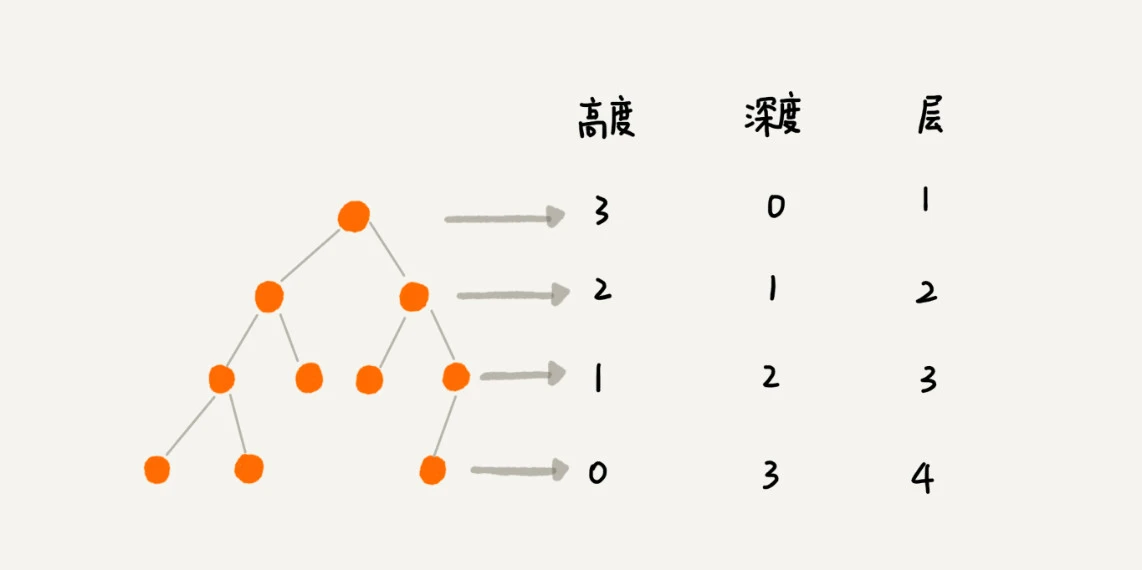
诀窍:高度是从下往上开始算;深度是从上往下开始算;层 = 深度 + 1
二叉树
定义:每个节点最多两个“叉”,即两个子节点,分为左、右子节点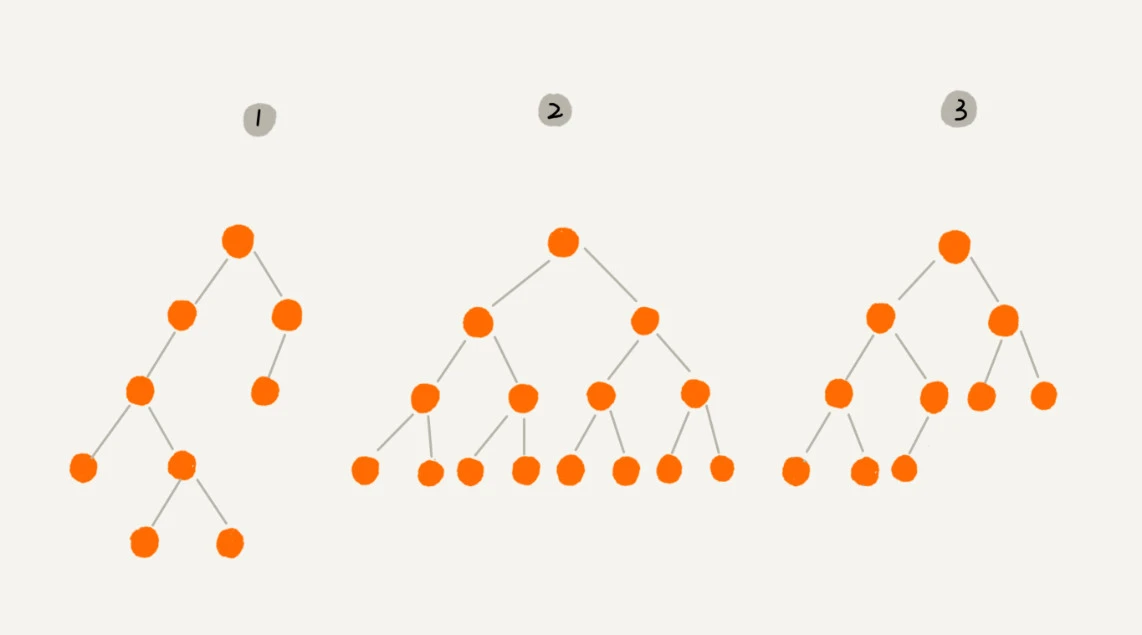
①:普通二叉树
②:满二叉树,叶子节点都在底层,并且每个节点都有两个子节点
③:完全二叉树,叶子节点都在最底下两层,最底层节点靠左排列,其他层节点数达最大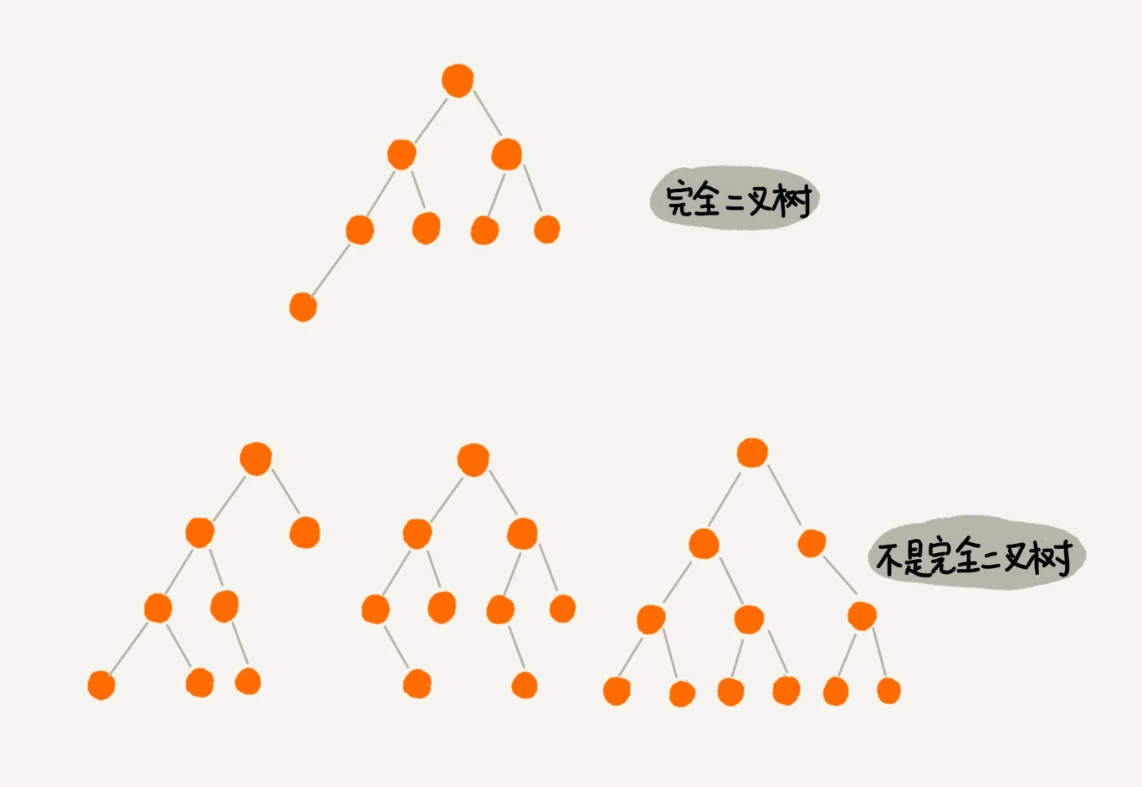
如何表示(或者存储)一棵二叉树?
一种是二叉链表(常用的),结构如下:使用 left、right 指针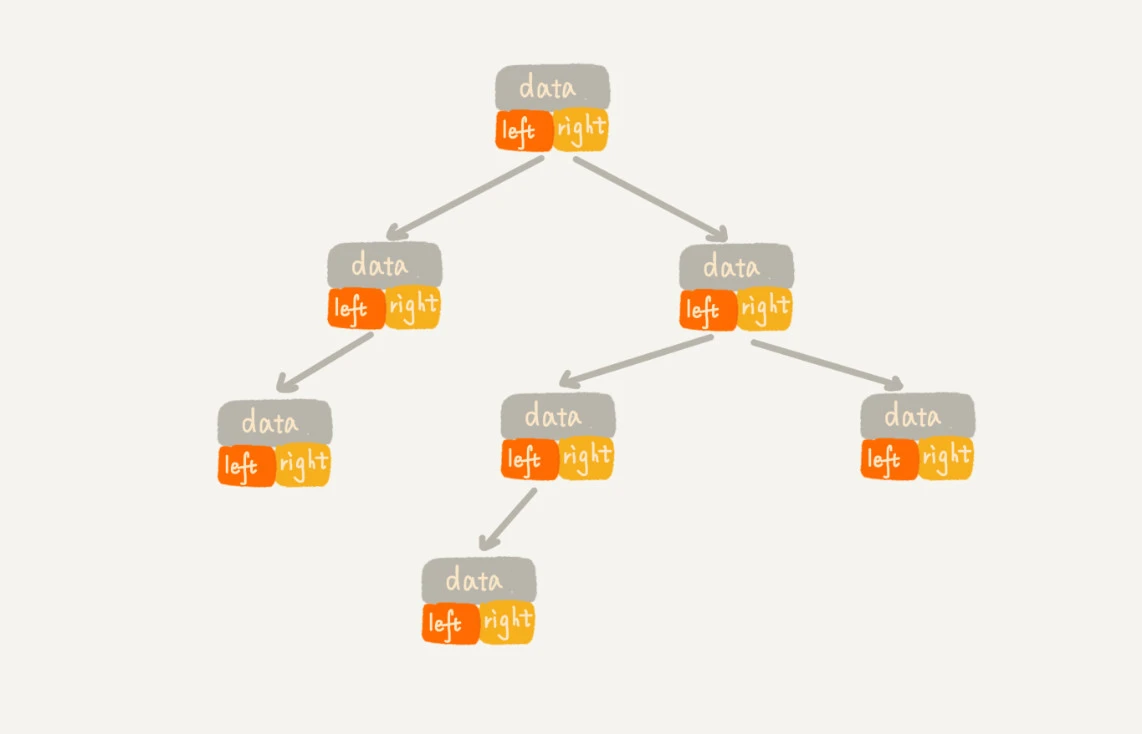
一种是数组顺序存储,结构如下:i 为父(根)节点下标,则左节点存在2 * i上,右节点存在2 * i + 1上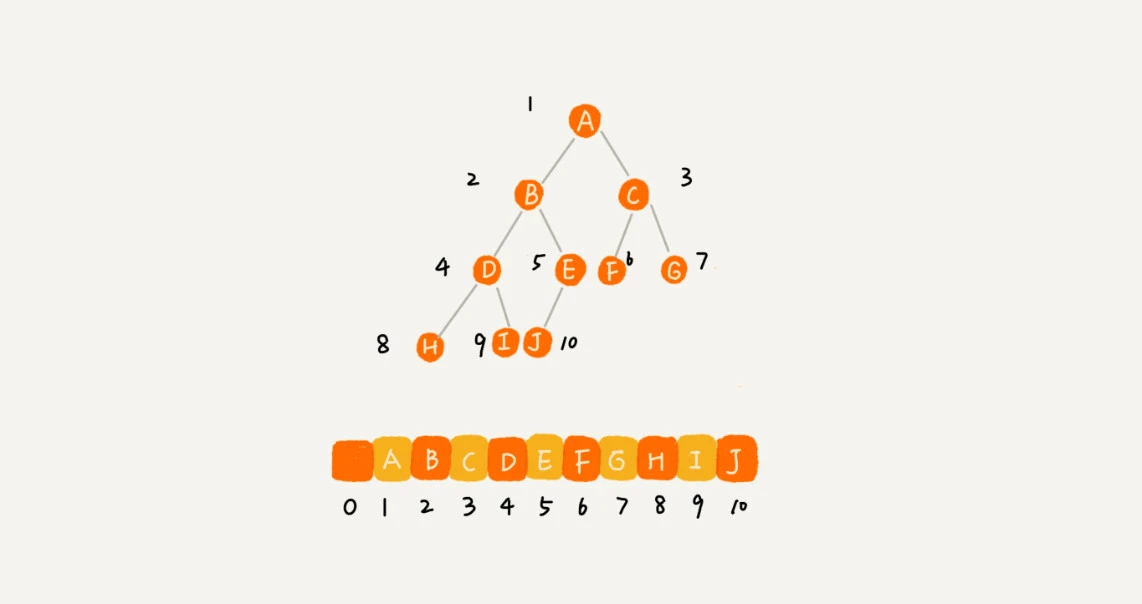
总结为:节点 X 存储下标为 i;其左结点存储在 2 * i 上;右节点存储在 2 * i + 1 上;其父节点存储在 i / 2 上。
所以数组存储时,知道了根节点位置就能找到整棵树节点位置。
二叉树的遍历
三种方式遍历:就是节点本身与左右子树的顺序
- 前序遍历:先打印节点本身,再打印左子树,最后打印右子树
- 中序遍历:先打印左子树,再打印节点本身,最后打印右子树
- 后序遍历:先打印左子树,再打印右子树,最后打印节点本身
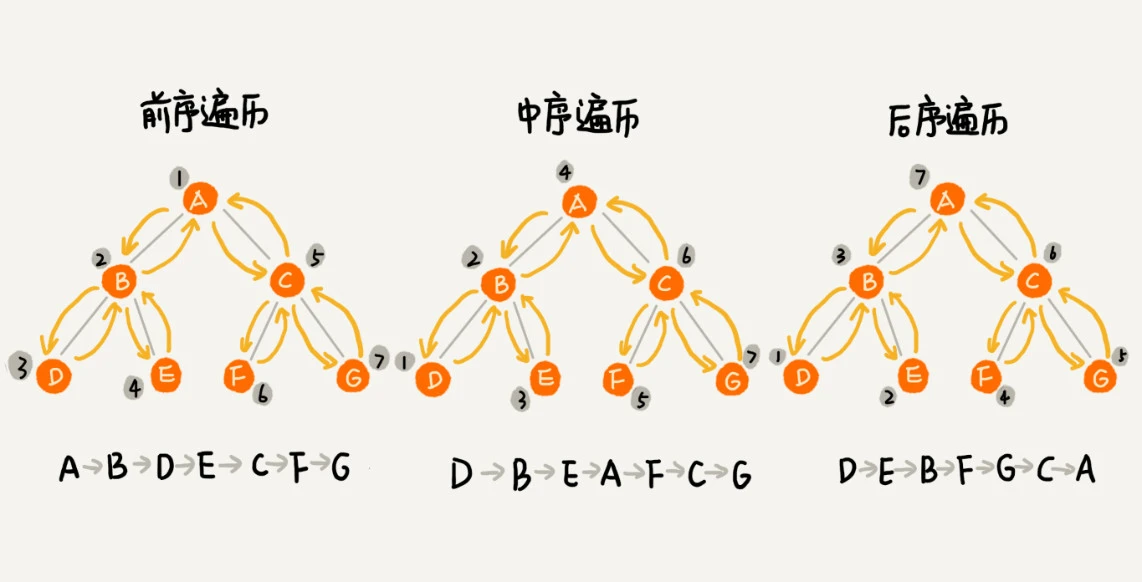
上述就是一个递归过程。
对应的递推公式为:
1 | |
对应的递归代码如下:
1 | |
时间复杂度为:O(n)
解答思考 & 内容总结
思考:二叉树有哪几种存储方式?什么样的二叉树适合用数组来存储?
解答:可以使用 数组、链表 存储
完全二叉树与满二叉树适合用数组存储,因为空闲元素更少。
新的思考
给定一组数据,比如 1,3,5,6,9,10,11,可以构建出多少种不同的完全二叉树?
我们讲了三种二叉树的遍历方式,前、中、后序。实际上,还有另外一种遍历方式,也就是按层遍历,你知道如何实现吗?
23、二叉树基础(上)
https://mrhzq.github.io/职业上一二事/算法学习/极客-数据结构与算法之美/数据结构/23、二叉树基础(上)/