12、排序（下）

思考：如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素？

主要内容

归并排序

原理：先将数据不停的平均分成两份，各自排序，最后组合，就成了一个排好序的数组了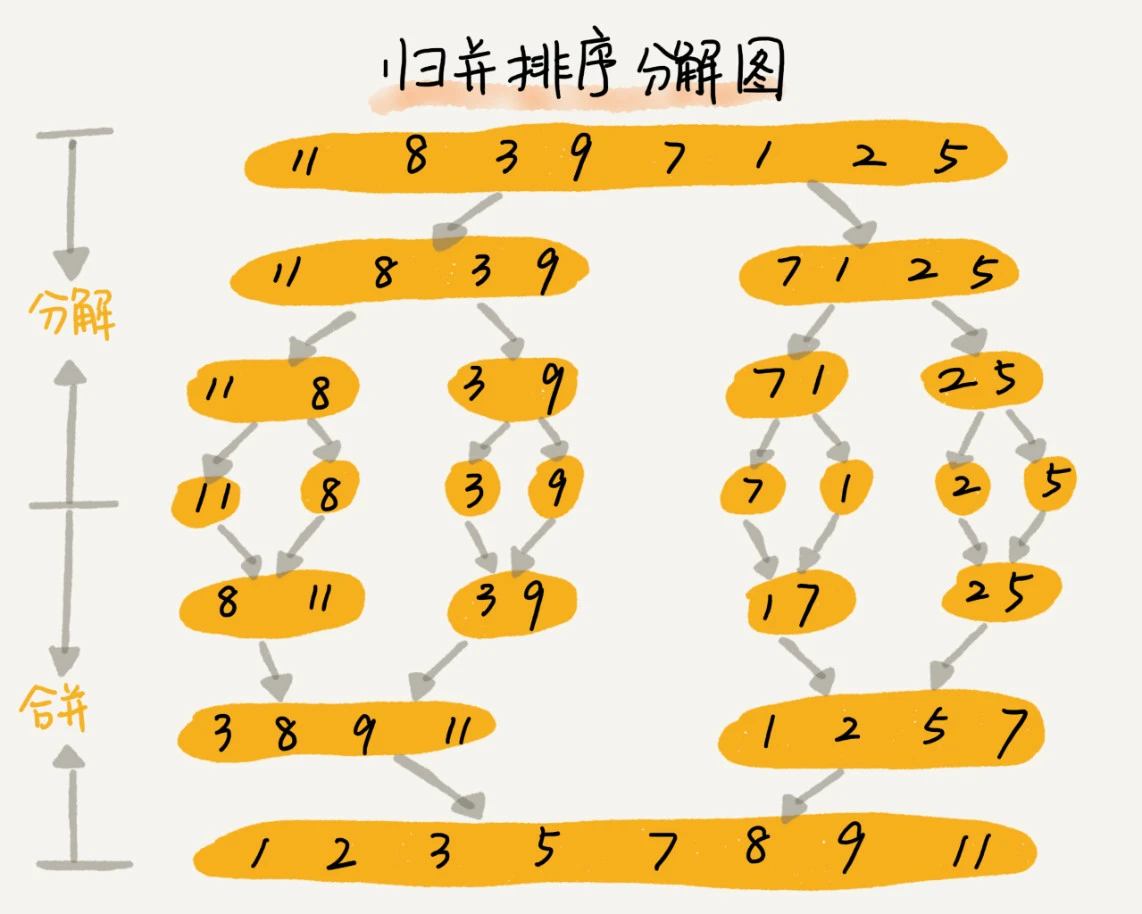

采用的是：分治思想，分而治之，将大问题化为小问题解决，小的解决后大的也就解决了
发现跟递归的思想很像，分治是处理问题的“思想”，递归是实现思想的“编程技巧”。

如何用递归实现归并排序？

递推公式：merge_sort(p……r) = merge(merge_sort(p……q), merge_sort(q+1……r))
终止条件：p >= r 不用再继续分解

使用 归并排序 手写实现 4，5，6，3，2，1 的升序

function merge_sort(A) {
  const n = A.length;
  merge_sort_c(A, 0, n - 1);
}

function merge_sort_c(A, p, r) {
  // 递归终止条件
  if (p >= r) {
    return;
  }

  // 取p到r之间的中间位置q
  const q = Math.floor((p + r) / 2);

  // 分治递归
  merge_sort_c(A, p, q);
  merge_sort_c(A, q + 1, r);

  // 将A[p...q]和A[q+1...r]合并为A[p...r]
  merge(A, p, q, r);
}

// 合并两个有序子数组
function merge(A, p, q, r) {
  // 初始化变量i, j, k
  let i = p, j = q + 1, k = 0;

  // 创建一个大小与A[p...r]相等的临时数组
  const tmp = new Array(r - p + 1);

  // 合并两个有序子数组
  while (i <= q && j <= r) {
    if (A[i] <= A[j]) {
      tmp[k++] = A[i++];
    } else {
      tmp[k++] = A[j++];
    }
  }

  // 判断哪个子数组中有剩余数据
  let start = i, end = q;
  if (j <= r) {
    start = j;
    end = r;
  }

  // 将剩余的数据拷贝到临时数组tmp
  while (start <= end) {
    tmp[k++] = A[start++];
  }

  // 将tmp中的数组拷贝回A[p...r]
  for (let i = 0; i <= r - p; i++) {
    A[p + i] = tmp[i];
  }
}

// 示例
const array = [5, 3, 8, 6, 1, 9, 2];
merge_sort(array);
console.log(array); // 输出：[1, 2, 3, 5, 6, 8, 9]

1. 归并排序是原地排序吗？
   1. 不是，因为它需要额外的存储空间，用来存储 tmp 数组，所以空间复杂度为 O(n)
2. 归并排序是稳定的排序算法吗？
   1. 是，遇到相同的元素，可以先把 left 中的元素放入，这样就能保证稳定
3. 归并排序的时间复杂度是多少？
   1. 由于使用了递归，所以先写出递归的时间复杂度推导公式：T(a) = T(b) + T(c) + K
      1. T(a) 代表解决总问题的时间
      2. T(b)、T(c) 代表解决子问题 b、c 的时间
      3. K 代表组合子问题 b、c 结果的时间
   2. 归并排序中：对于 n 个数据，组合的平均时间为 O(n)，因为组合最好时间为 n/2，最坏时间为 n - 1，所以平均时间为 O((n/2+n-1)2) 去掉常量就为 O(n)
   3. 所以 T(n) = T(n/2) + T(n/2) + n

// 展开后如下：
T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
     = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
     ......
     = 2^k * T(n/2^k) + k * n
     ......

4. 最终得到 T(n) = Cn + nlog2n，去掉常量最终为 O(nlogn)
5. 并且归并排序与原始数据是否排序无关，所以它的时间复杂度很稳定

快速排序

原理：还是采用分治思想，是以任意元素为分治点，然后将小于该元素的放在左边，大于该元素的放在右边，该元素放在中间。然后再递归排序左右两边，最后再组合一下就行。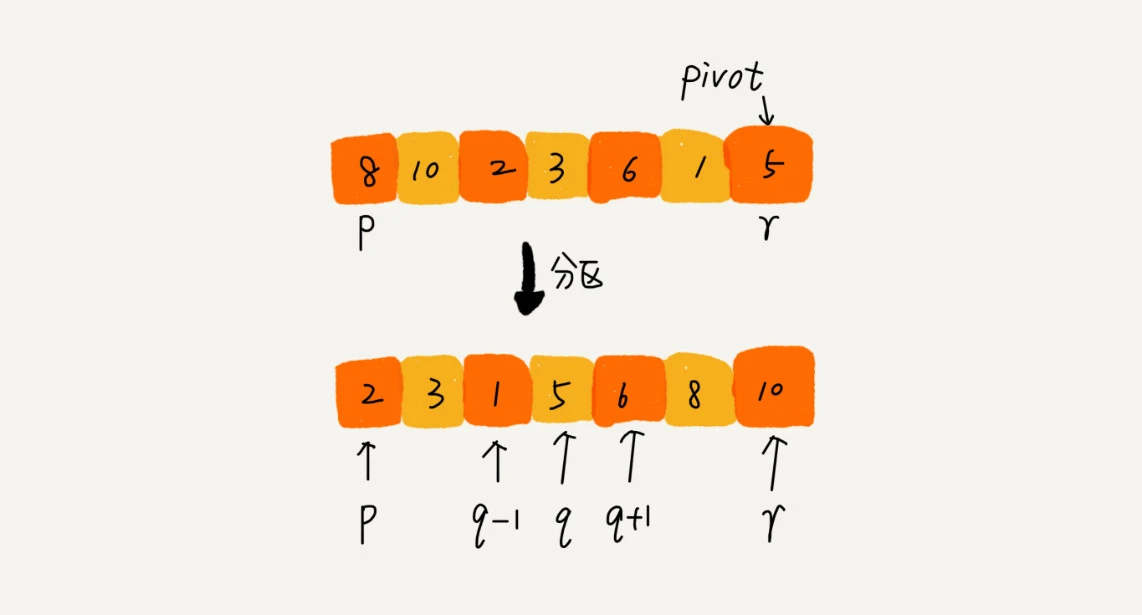

递推公式：quick_sort(p……r) = quick_sort(p……q-1) + quick_sort(q+1…… r)
终止条件：p >= r

使用 快速排序 手写实现 4，5，6，3，2，1 的升序

function quickSort(A, p = 0, r = A.length - 1) {
  if (p < r) {
    const q = partition(A, p, r); // 获取分区后的分割点
    quickSort(A, p, q - 1); // 递归对左子数组进行排序
    quickSort(A, q + 1, r); // 递归对右子数组进行排序
  }
  return A;
}

// partition函数
function partition(A, p, r) {
  const pivot = A[r];
  let i = p;

  for (let j = p; j < r; j++) {
    if (A[j] < pivot) {
      [A[i], A[j]] = [A[j], A[i]]; // 使用解构赋值进行交换
      i++;
    }
  }

  [A[i], A[r]] = [A[r], A[i]]; // 将基准元素放在正确的位置
  return i;
}

// 示例
const unsortedArray = [5, 3, 8, 1, 2, 7, 6, 9];
console.log(quickSort(unsortedArray)); // 输出：[1, 2, 3, 5, 6, 7, 8, 9]

以下是分区的过程：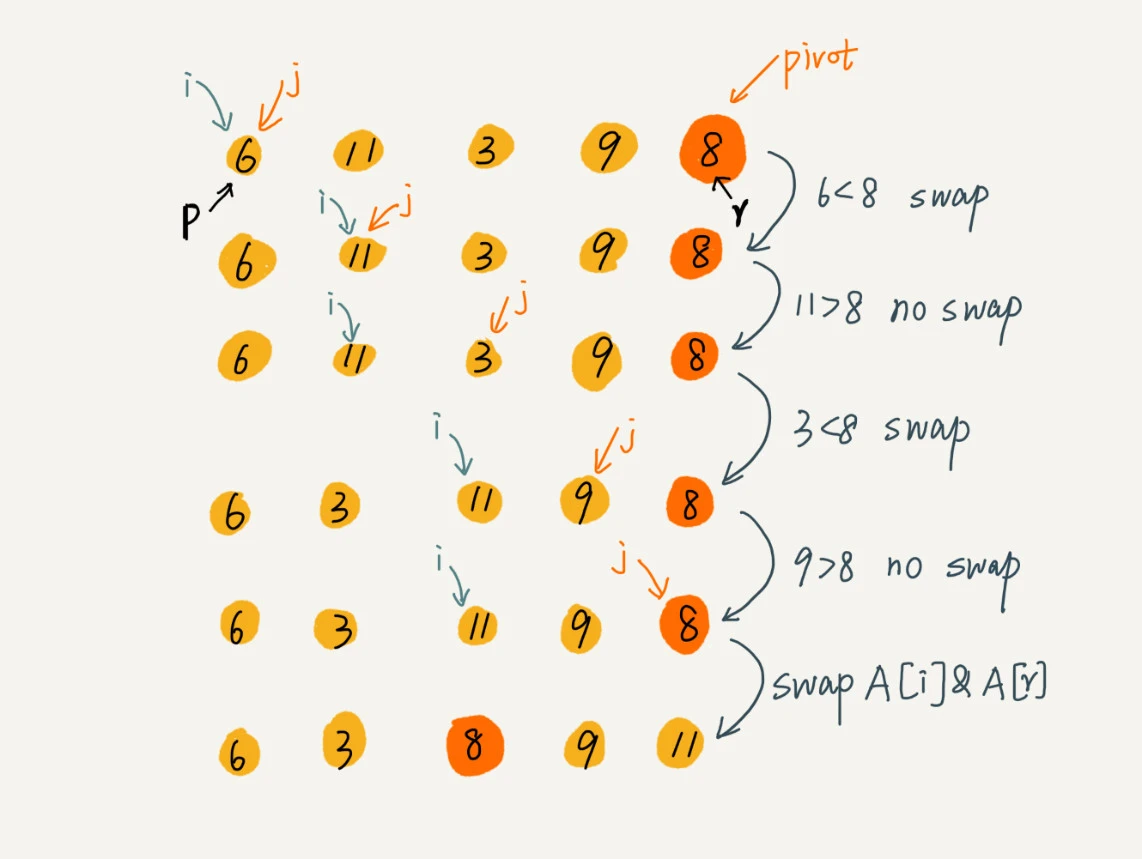

1. 快速排序是原地排序吗？
   1. 是，因为不需要额外的存储空间，所以空间复杂度为 O(1)
2. 快速排序是稳定的排序算法吗？
   1. 不是
3. 快速排序的时间复杂度是多少？
   1. 由于使用了递归，所以先写出递归的时间复杂度推导公式：T(a) = T(b) + T(c) + K
      1. T(a) 代表解决总问题的时间
      2. T(b)、T(c) 代表解决子问题 b、c 的时间
      3. K 代表组合子问题 b、c 结果的时间
   2. T(n) = T(a) + T(c) + O(1)
   3. 所以 T(n) = T(n/2) + T(n/2) + n
   4. 求解并去掉常量后为 O(nlogn)
   5. 但若数据已排序，那每次选择最后一个分区，则恶化为 O(n^2)

归并与快排的区别

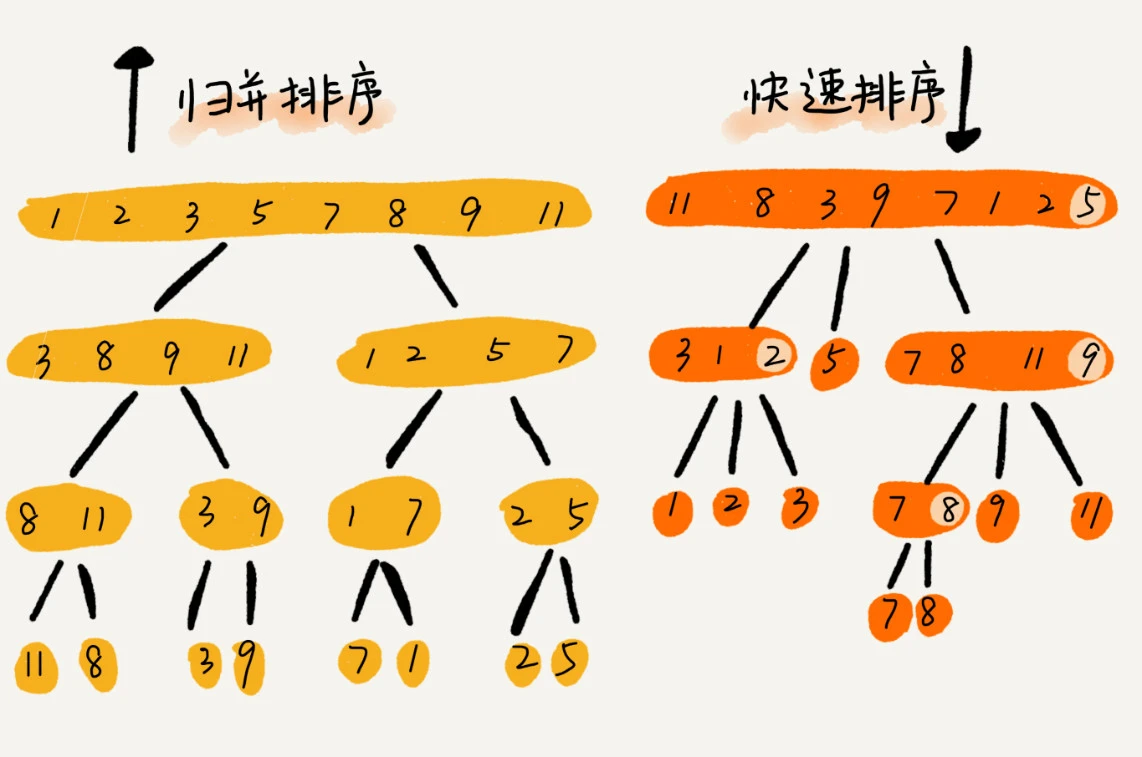
归并：自底向上，它在最底部才处理排序，然后向上再合并处理已排序的子数据
快排：自顶向下，它在分区的时候就开始再处理排序了，然后向上合并时不做任何处理

解答思考

思考：如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素？
使用分治思想，将数据以最后一个元素分区，大于它的在左侧，小于它的在右侧，最终分为 List[0…p-1], List[p], List[p+1……len]
若 p+1 = K，则 List[p] 就是第 K 大的元素
若 p+1 > K，则在左侧 List[0…p-1] 里面重新以最后一个元素分区再找，直到找到
若 p+1 < K，则在右侧 List[p+1…len] 里面重新以最后一个元素分区再找，直到找到
最终时间复杂度为：O(n)
因为第一次分区遍历 n 次，第二次分区遍历 n/2 次，第三次分区遍历 n/4……
最终和为 2n-1，去掉常量就为 O(n)
递推公式：getK(p…r) = getK(0…p-1)+getK(p+1…r)，k = p+1

function getKValue(List, k, p = 0, r = List.length) {
  const q = partition(List, p, r); // 获取分区后的分割点下标

  if(q+1 === k) return q
  else if(q + 1 > k){
    getKValue(List, k, p, q - 1)
  } else {
    getKValue(List, k, q + 1, r)
  }
}

function partition(List, p, r) {
  const point = List[r - 1]
  let i = p

  for(let j = p; j < r; j++) {
    if(List[j] > point) {
      [List[i], List[j]] = [List[j], List[i]]; // 使用解构赋值进行交换
      i++;
    }
  }

  [List[i], List[r]] = [List[r], List[i]]; // 将基准元素放在正确的位置
  return i;
}

内容总结

归并排序关键：merge_sort(p...r) = merge(merge_sort(p...q), merge_sort(q+1...r)), p >= r 终止，其中的 merge 函数是关键

快速排序关键：quick_sort(p...r) = quick_sort(p...q-1) + quick_sort(q+1...r), p >= r 终止，其中的 partition 函数式关键

新的思考

现在你有 10 个接口访问日志文件，每个日志文件大小约 300MB，每个文件里的日志都是按照时间戳从小到大排序的。你希望将这 10 个较小的日志文件，合并为 1 个日志文件，合并之后的日志仍然按照时间戳从小到大排列。如果处理上述排序任务的机器内存只有 1GB，你有什么好的解决思路，能“快速”地将这 10 个日志文件合并吗？